Mojo The next AI language ? Jean-L uc T ROMPA RENT HE LL OWO RK
A presentation at Salon de la DATA in September 2024 in Nantes, France by Jean-Luc Tromparent

Mojo The next AI language ? Jean-L uc T ROMPA RENT HE LL OWO RK
Use Case Value Proposition

What is The current language of AI ?

Chat GPT Advisor L’IA, ou intelligence artificielle, peut être développée et programmée dans différents langages de programmation. Certains des langages les plus couramment utilisés pour créer des systèmes d’IA incluent Python, Java, C++, et R, entre autres. Python est particulièrement populaire dans le domaine de l’IA en raison de sa simplicité, de sa flexibilité, de sa large gamme de bibliothèques et de frameworks dédiés à l’IA (comme TensorFlow, PyTorch, scikit-learn, etc.), et de sa communauté active de développeurs.
StackOverflow Advisor
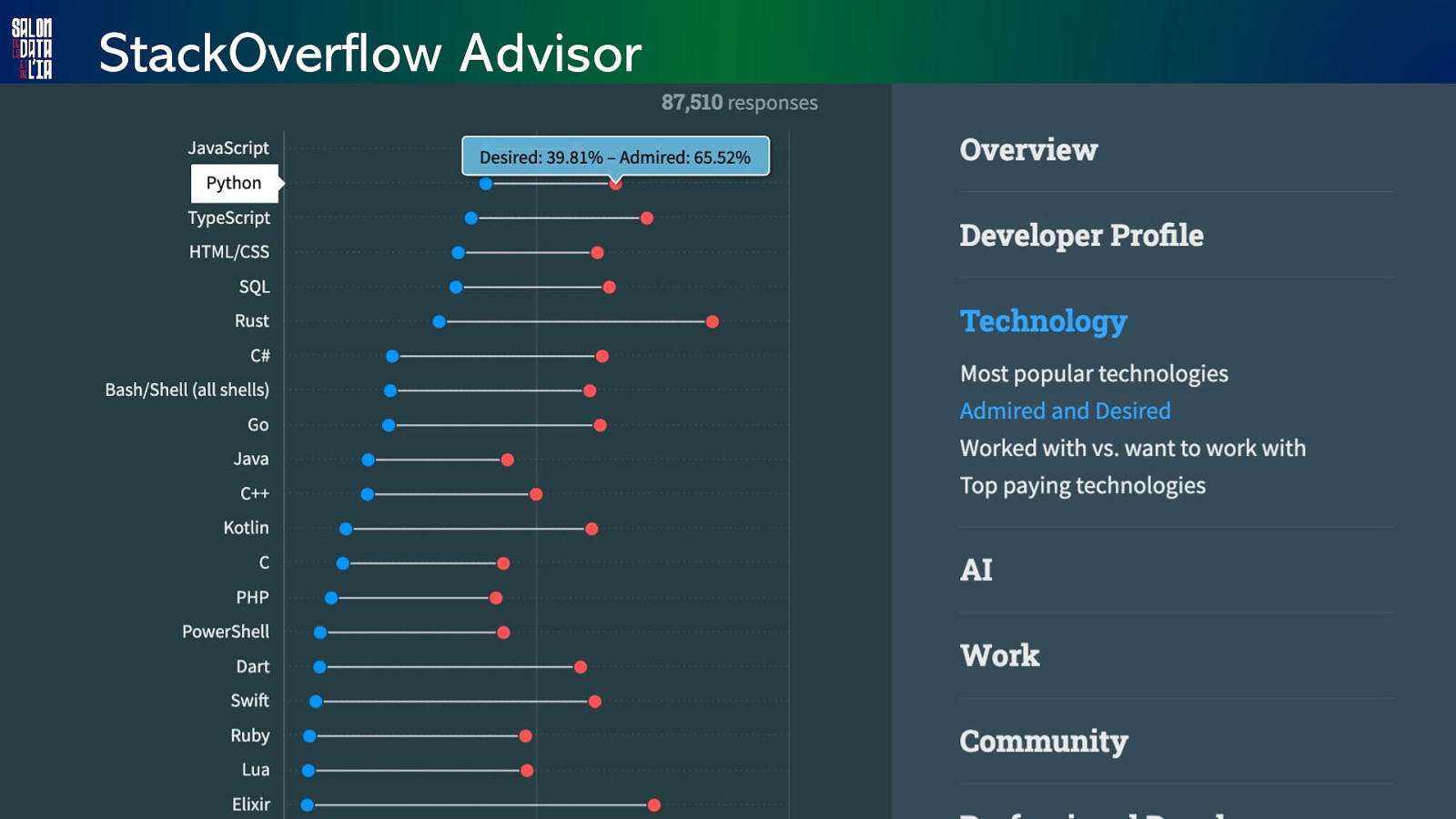
StackOverflow Advisor
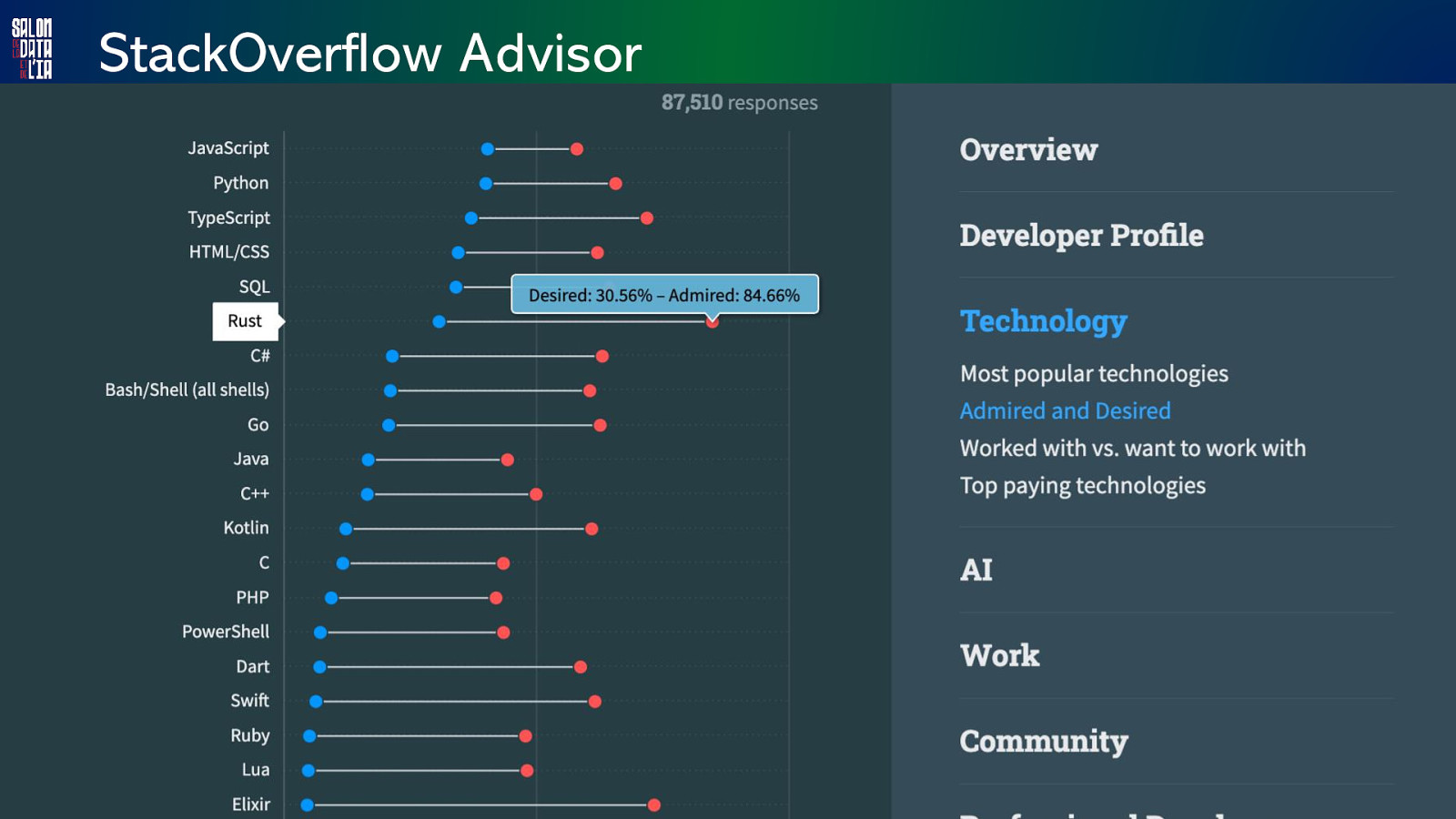
StackOverflow Advisor
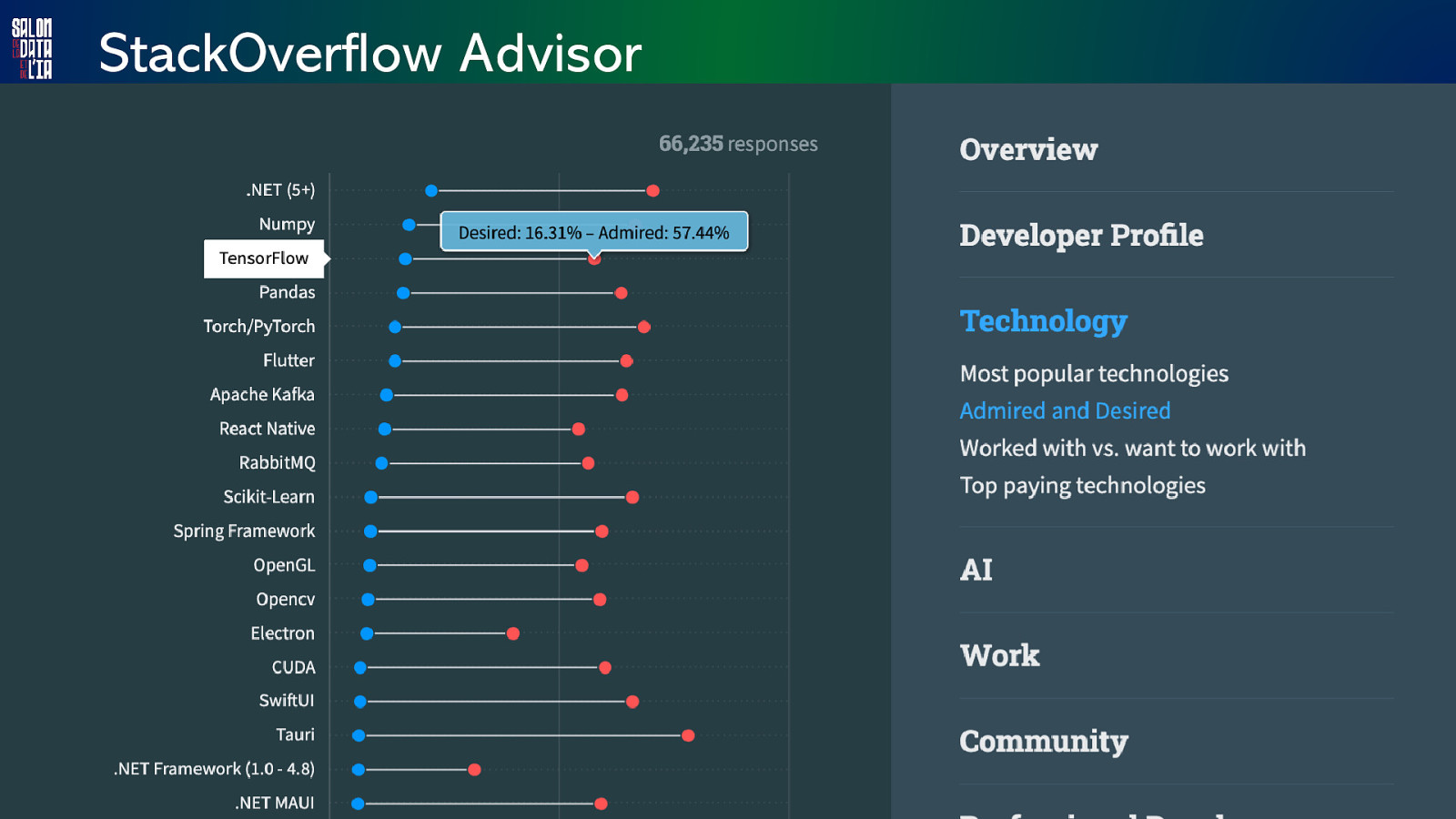
StackOverflow Advisor
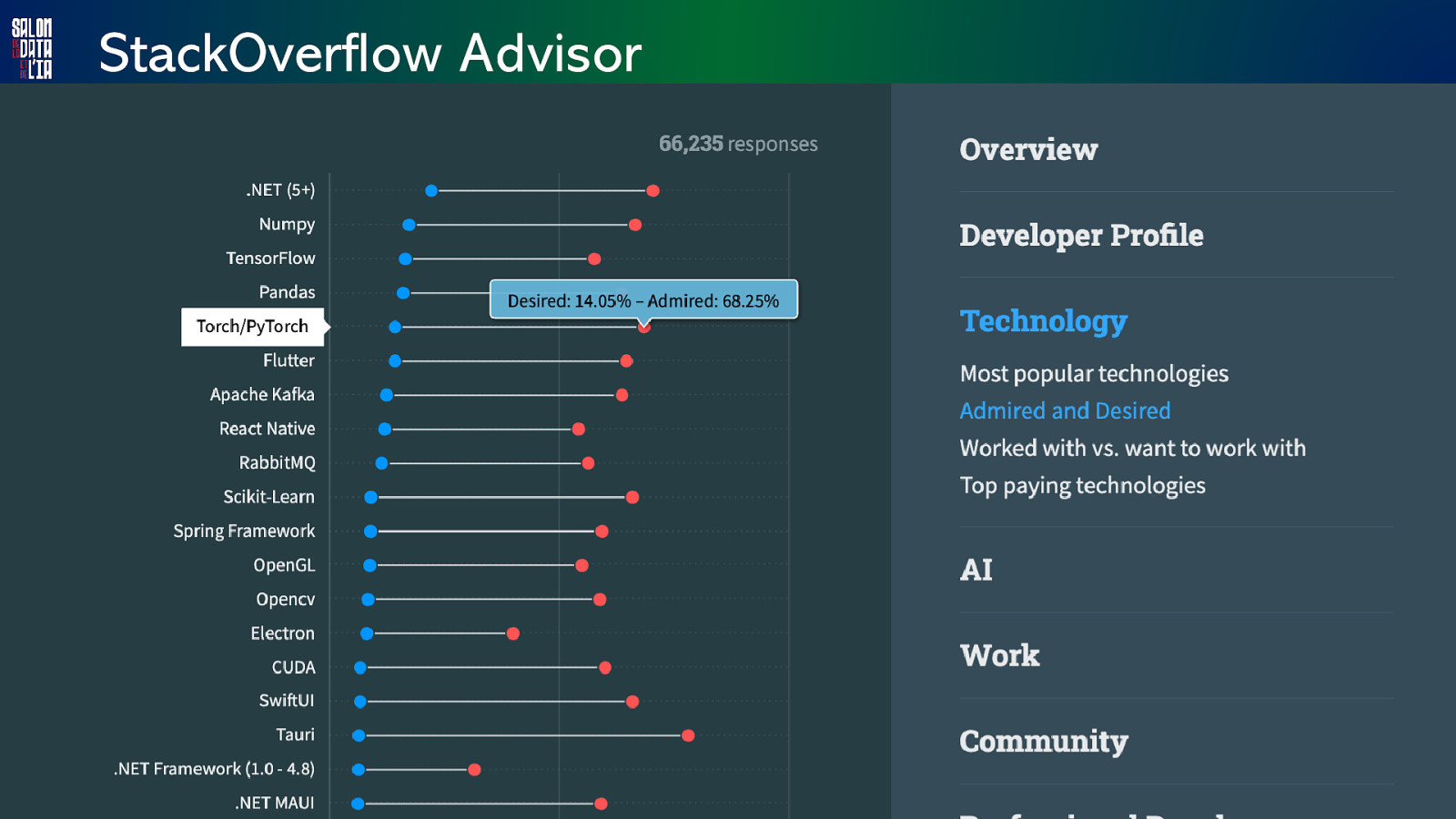
StackOverflow Advisor
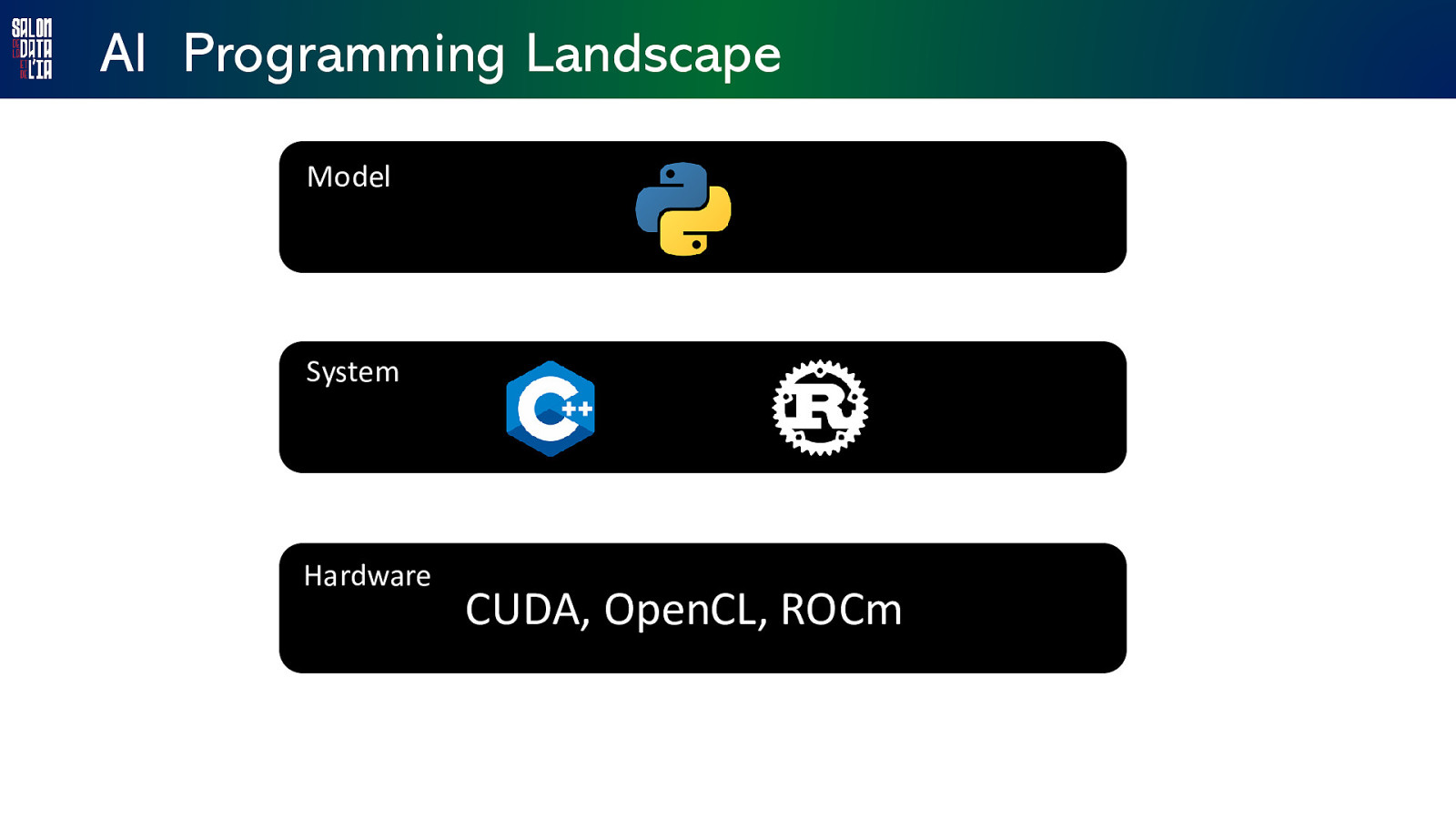
AI Programming Landscape Model System Hardware CUDA, OpenCL, ROCm

NEW Kid in ToWN ! Mojo 02/05/2023
Mojo is born ! https://www.modular.com/blog/the-future-of-ai-depends-on-modularity

Mojo is born ! Modular Accelerated eXecution platform https://www.modular.com/blog/a-unified-extensible-platform-to-superpower-your-ai

Mojo is born ! • Member of the python family (superset of python) • Support modern chip architectures (thanks to MLIR) • Predictable low level performance https://www.modular.com/blog/a-unified-extensible-platform-to-superpower-your-ai

Mojo is born ! Chris Lattner 2000 beginning of the project LLVM 2003 release of LLVM 1.0 2007 release of CLang 1.0 2008 XCode 3.1 2011 Clang replace gcc on macos 2014 release of Swift 1.0 2018 beginning of the MLIR 2022 creation of Modular cie 2023 https://www.nondot.org/sabre/
Mojo is blazing fast ! https://www.modular.com/blog/how-mojo-gets-a-35-000x-speedup-over-python-part-1

Mojo is blazing fast ! Changelog https://www.modular.com/blog/how-mojo-gets-a-35-000x-speedup-over-python-part-1 2022/01 incorporation 2022/07 seed round (30 M$) 2023/05 announce MAX & Mojo 2023/08 serie B (100 M$) 2023/09 release mojo 0.2.1 2023/10 release mojo 0.4.0 .. 2024/01 release mojo 0.7.0 2024/02 release MAX & mojo 24.1 2024/06 release MAX & mojo 24.4
Mojo is blazing fast ! https://www.modular.com/blog/how-mojo-gets-a-35-000x-speedup-over-python-part-1

Performance matters ! Performance matters : • for our users

Performance matters ! Your resume is being processed

Performance matters ! Performance matters : • for our users • for (artificial) intelligence
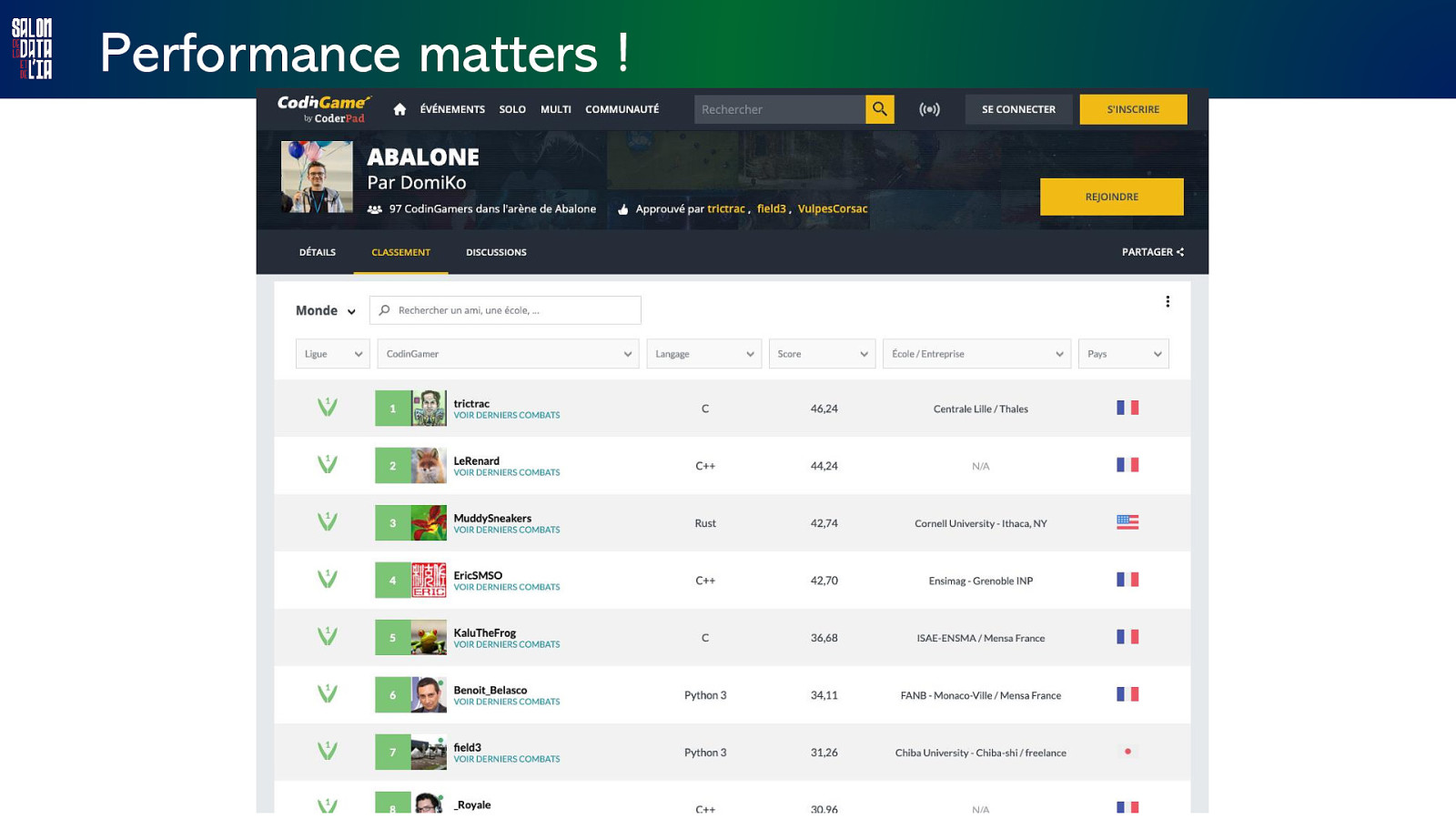
Performance matters !

Performance matters ! Performance matters : • for our users • for (artificial) intelligence • for the planet
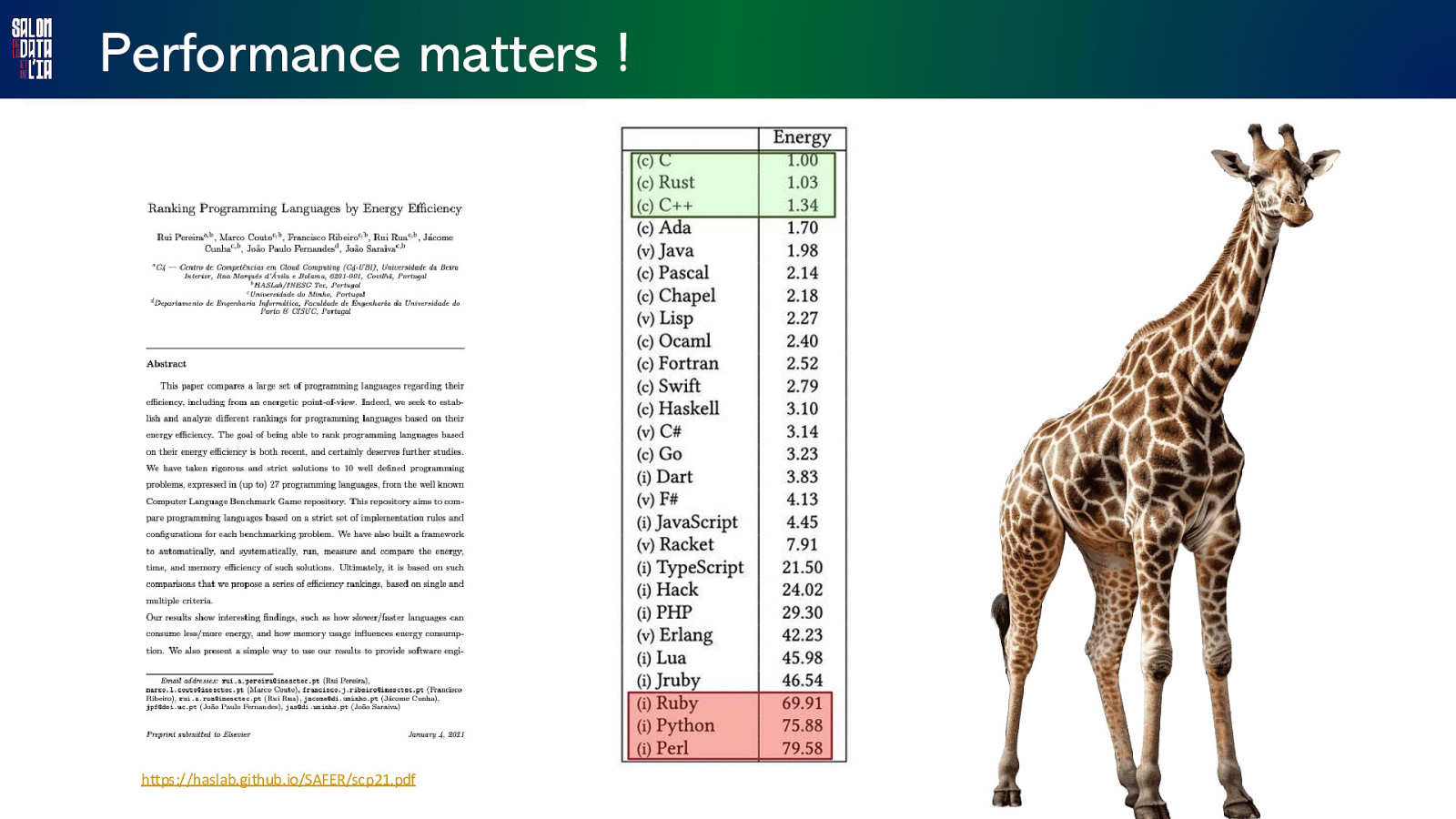
Performance matters ! https://haslab.github.io/SAFER/scp21.pdf
Meetup python-rennes https://www.meetup.com/fr-FR/python-rennes/ https://www.youtube.com/watch?v=gE6HUsmh554

Performance matters ! Performance matters : • for our users • for (artificial) intelligence • for the planet

it’s demo time ! Laplacian filter (edge detection)

Edge Detection

Edge Detection kernel Convolve
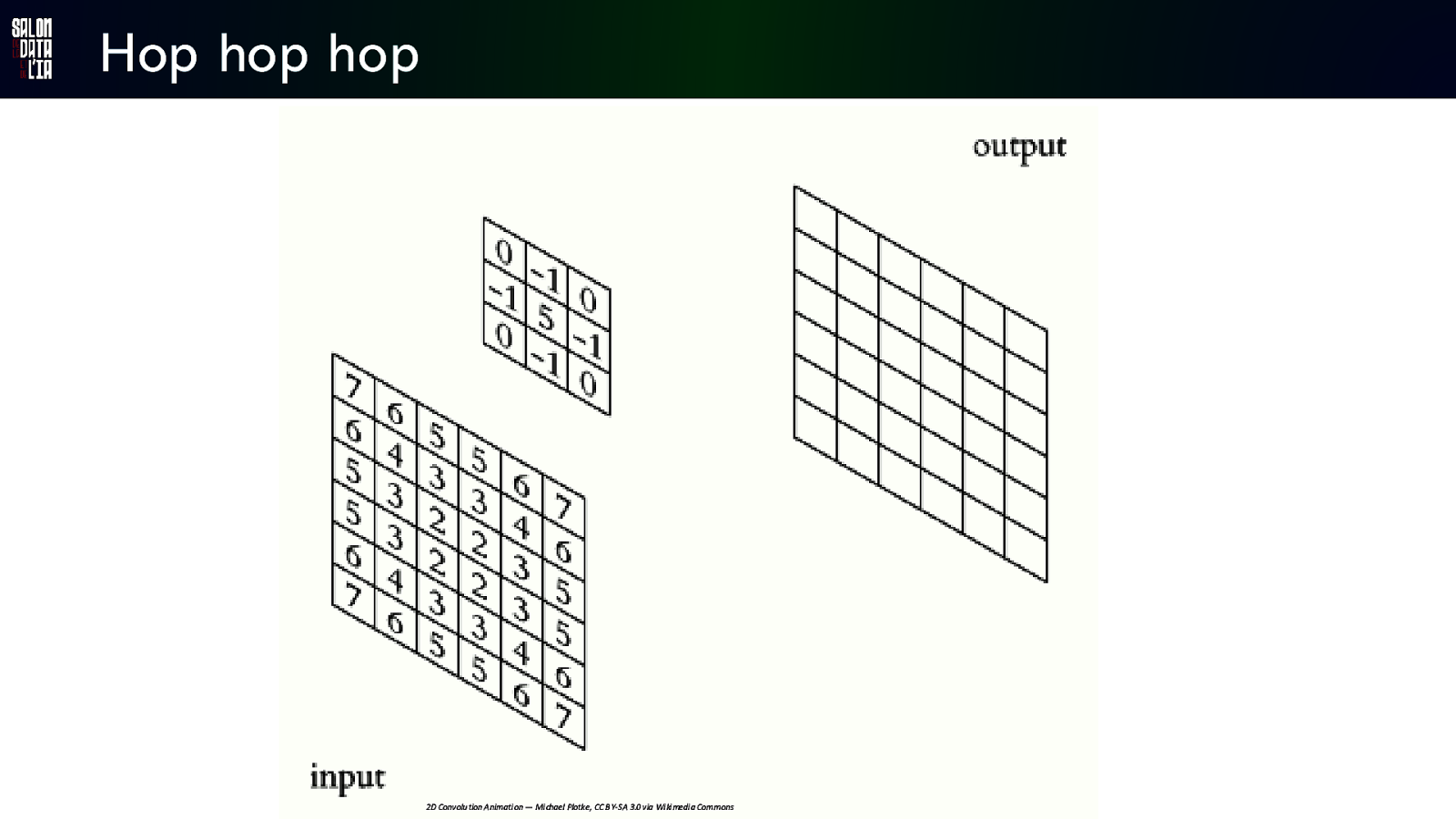
Hop hop hop 2D Convolu tion Animati on — Mi chael Plotke, CC B Y-SA 3.0 via Wi ki medi a Commons
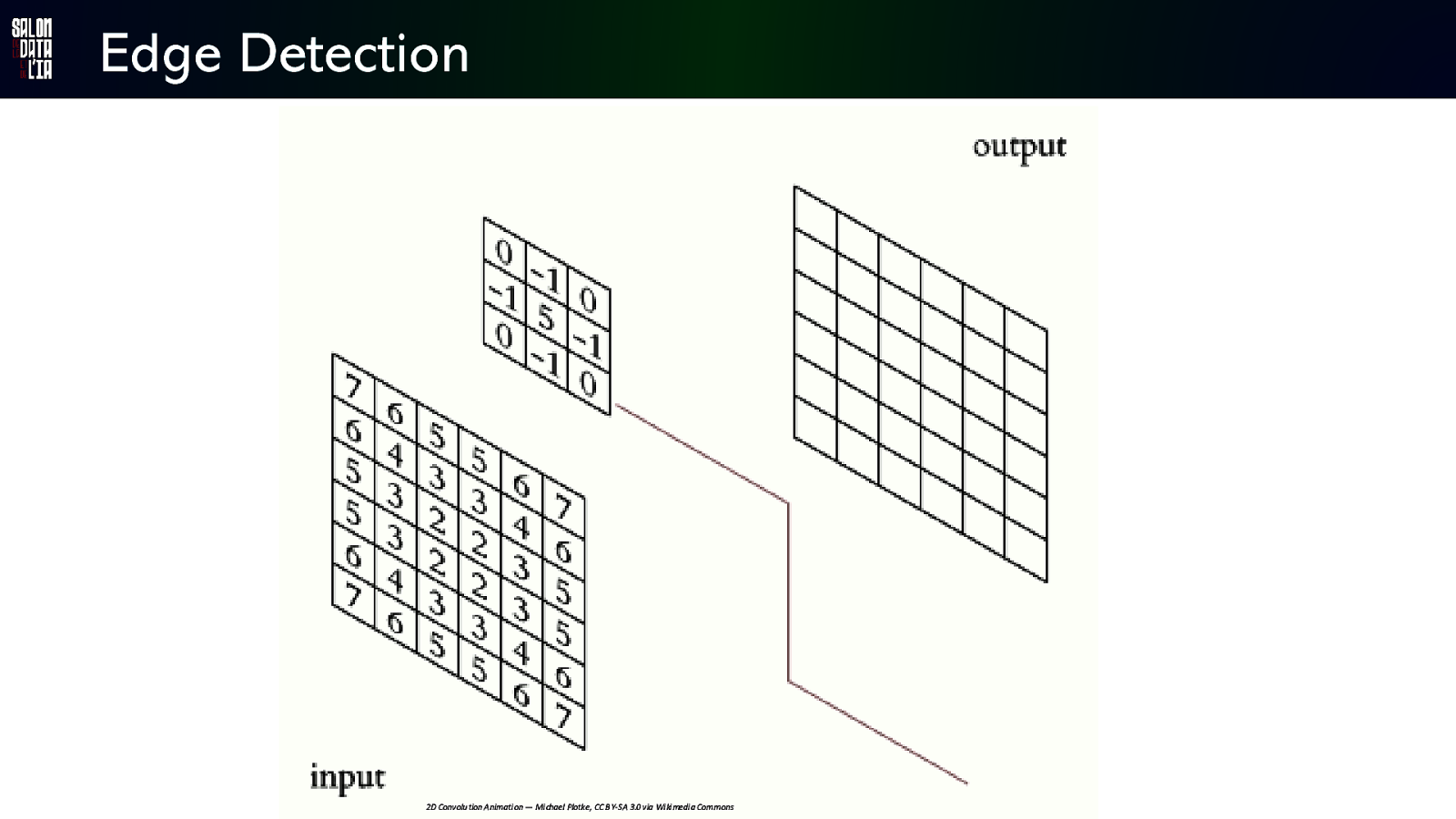
Edge Detection 2D Convolu tion Animati on — Mi chael Plotke, CC B Y-SA 3.0 via Wi ki medi a Commons
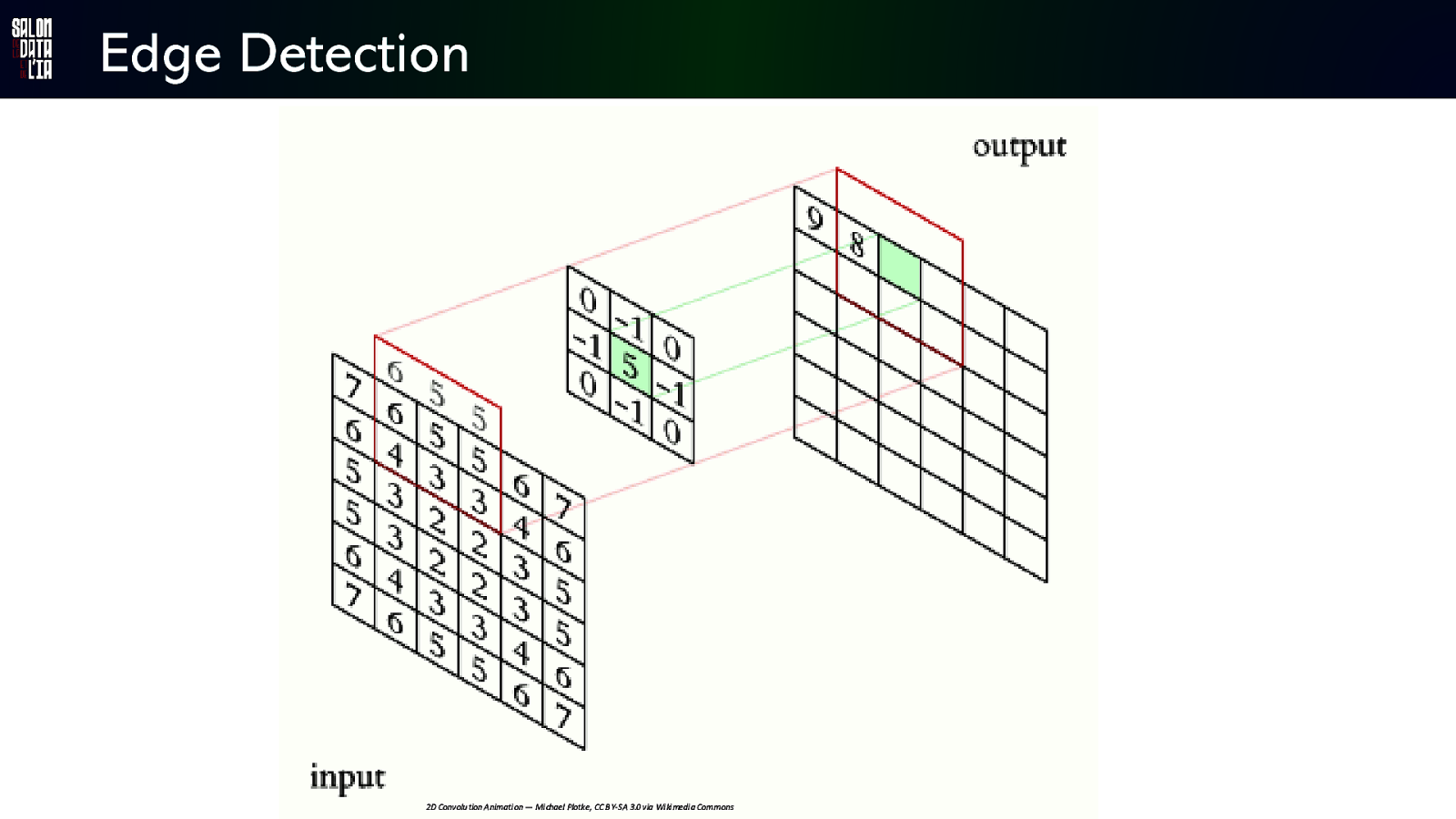
Edge Detection 2D Convolu tion Animati on — Mi chael Plotke, CC B Y-SA 3.0 via Wi ki medi a Commons

it’s demo time ! Python implementations

naïve version : 500 ms numpy mul : 250 ms numpy+numba : 50 ms Recap opencv : 0.5 ms x2 x 10 x 1000 And now in mojo ?
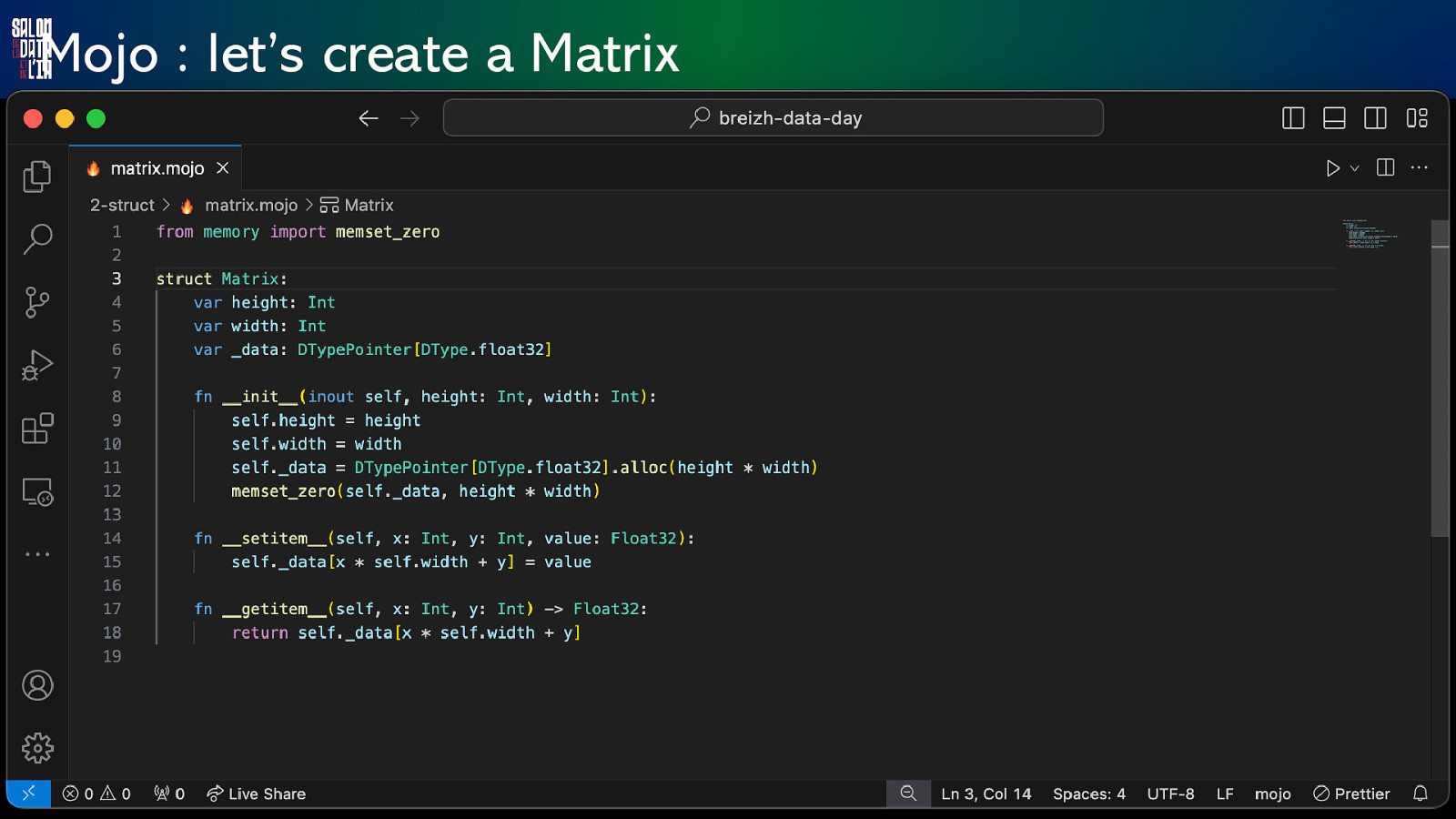
Mojo : let’s create a Matrix
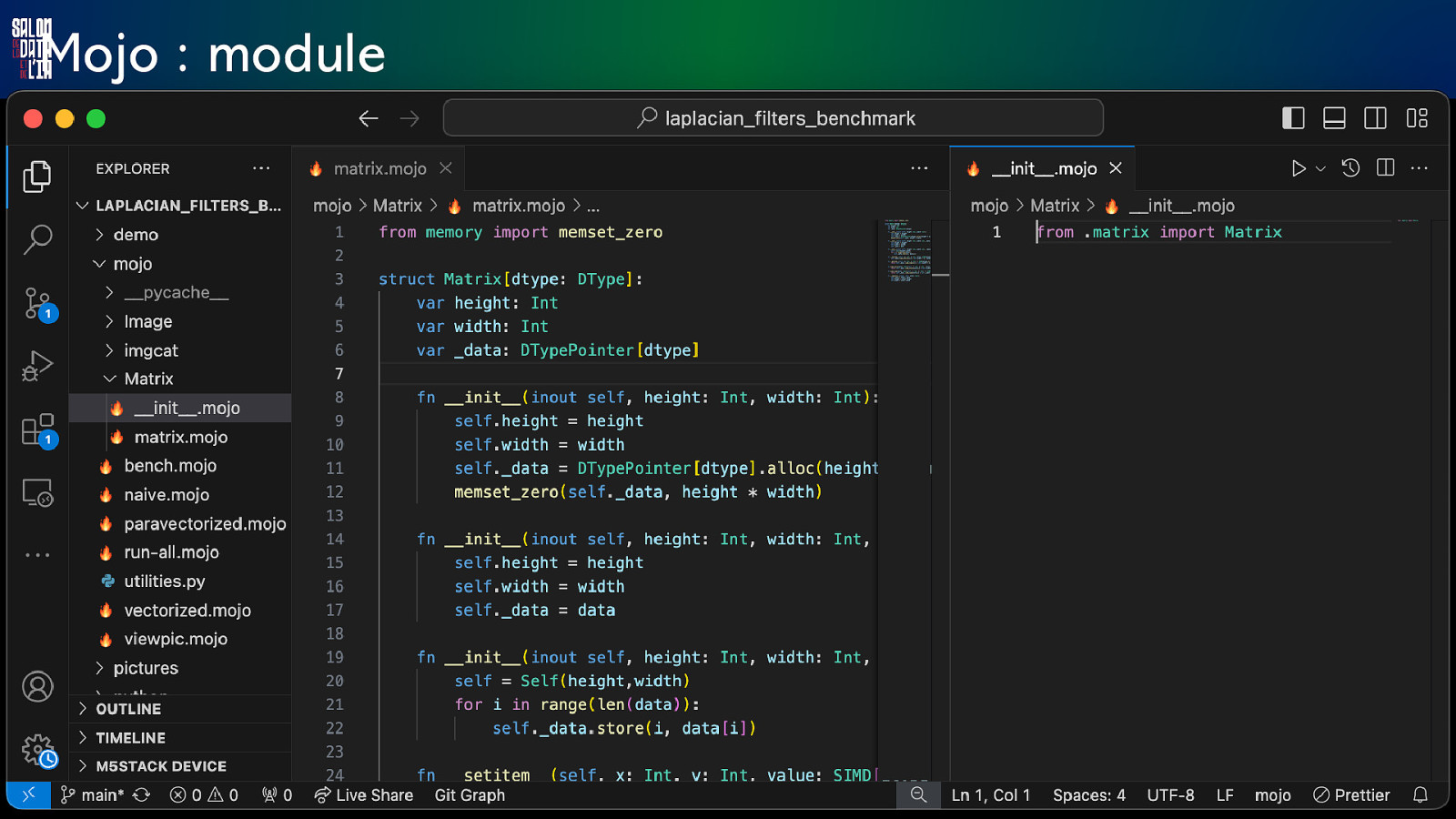
Mojo : module
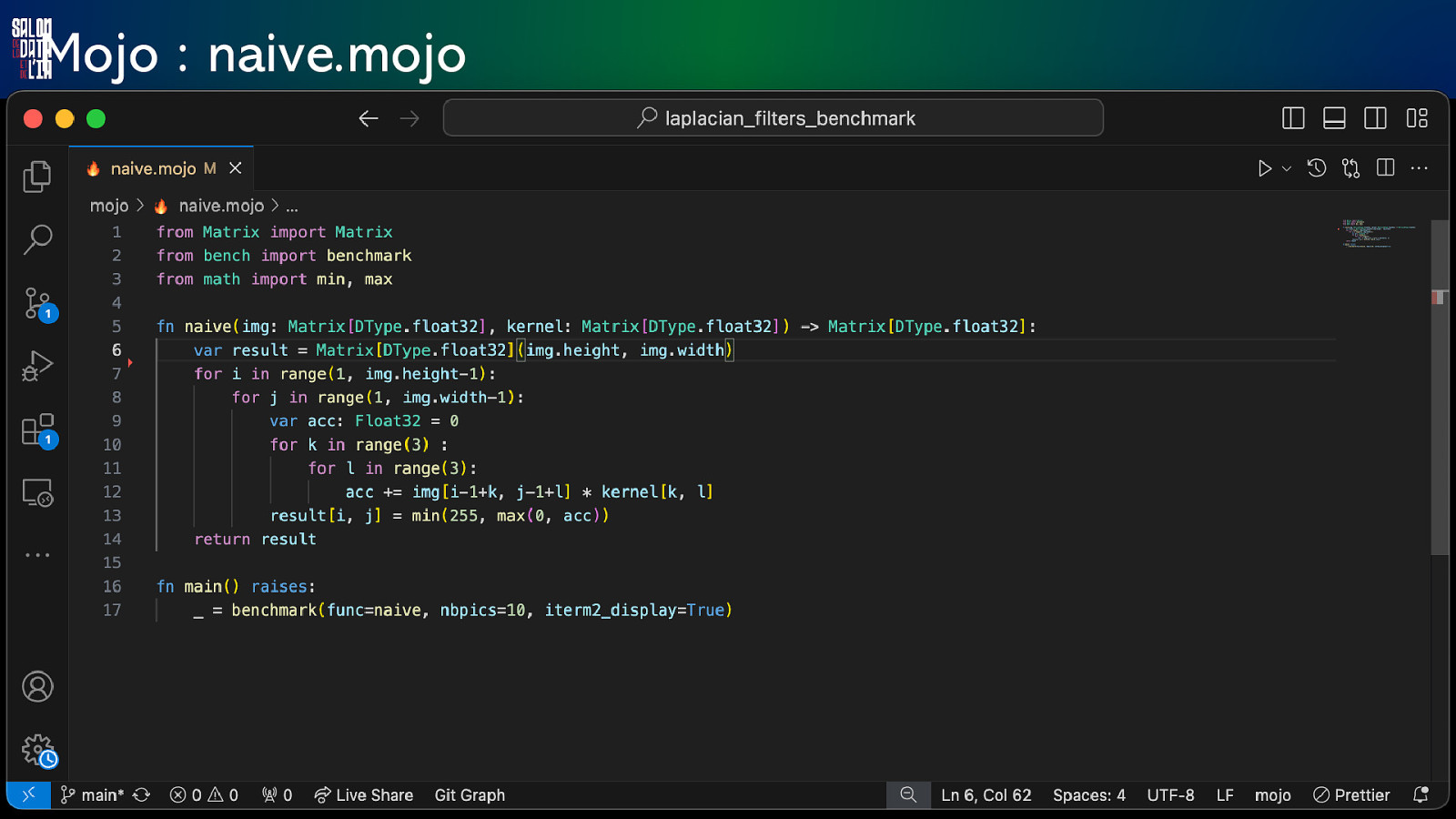
Mojo : naive.mojo
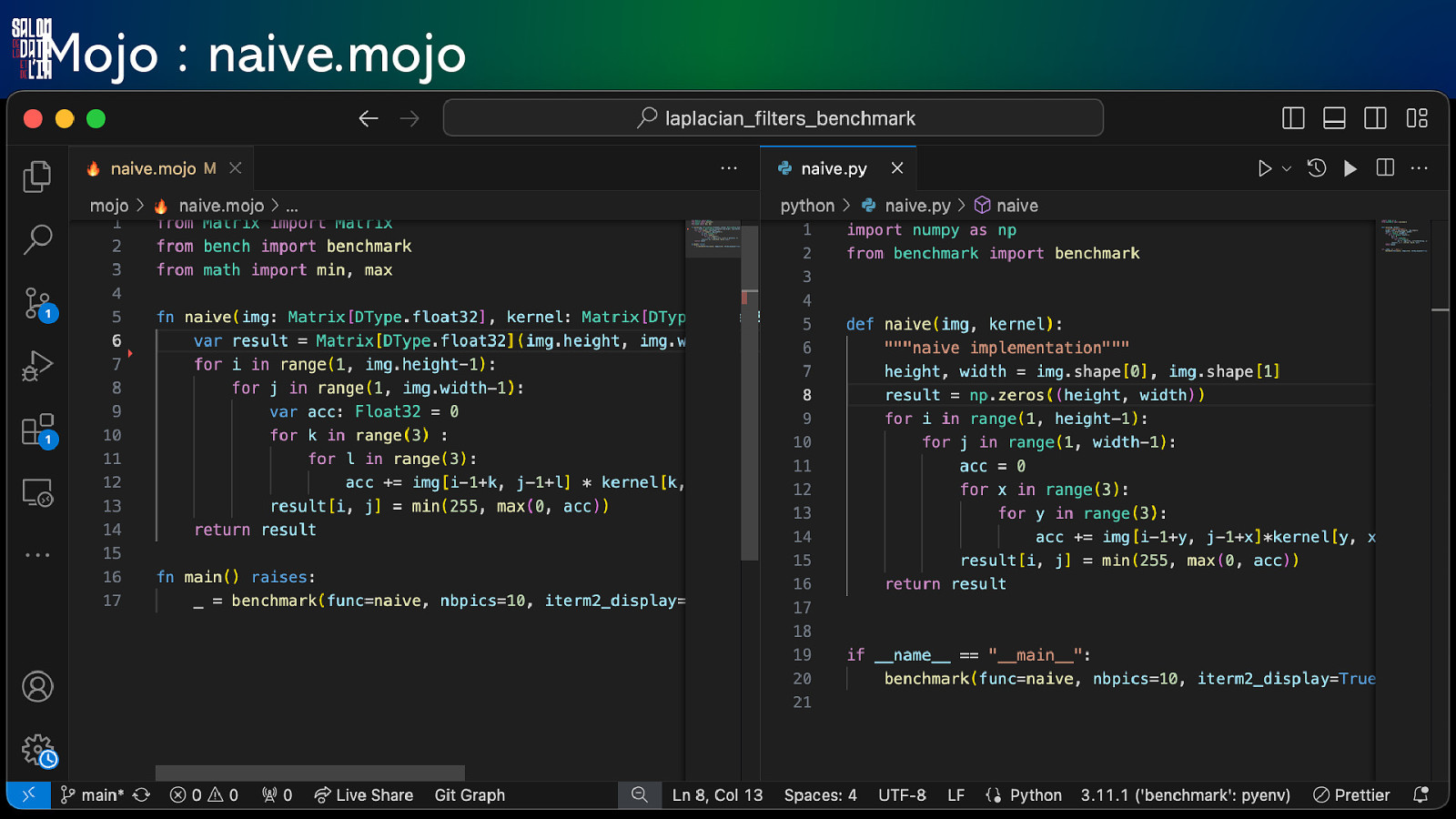
Mojo : naive.mojo
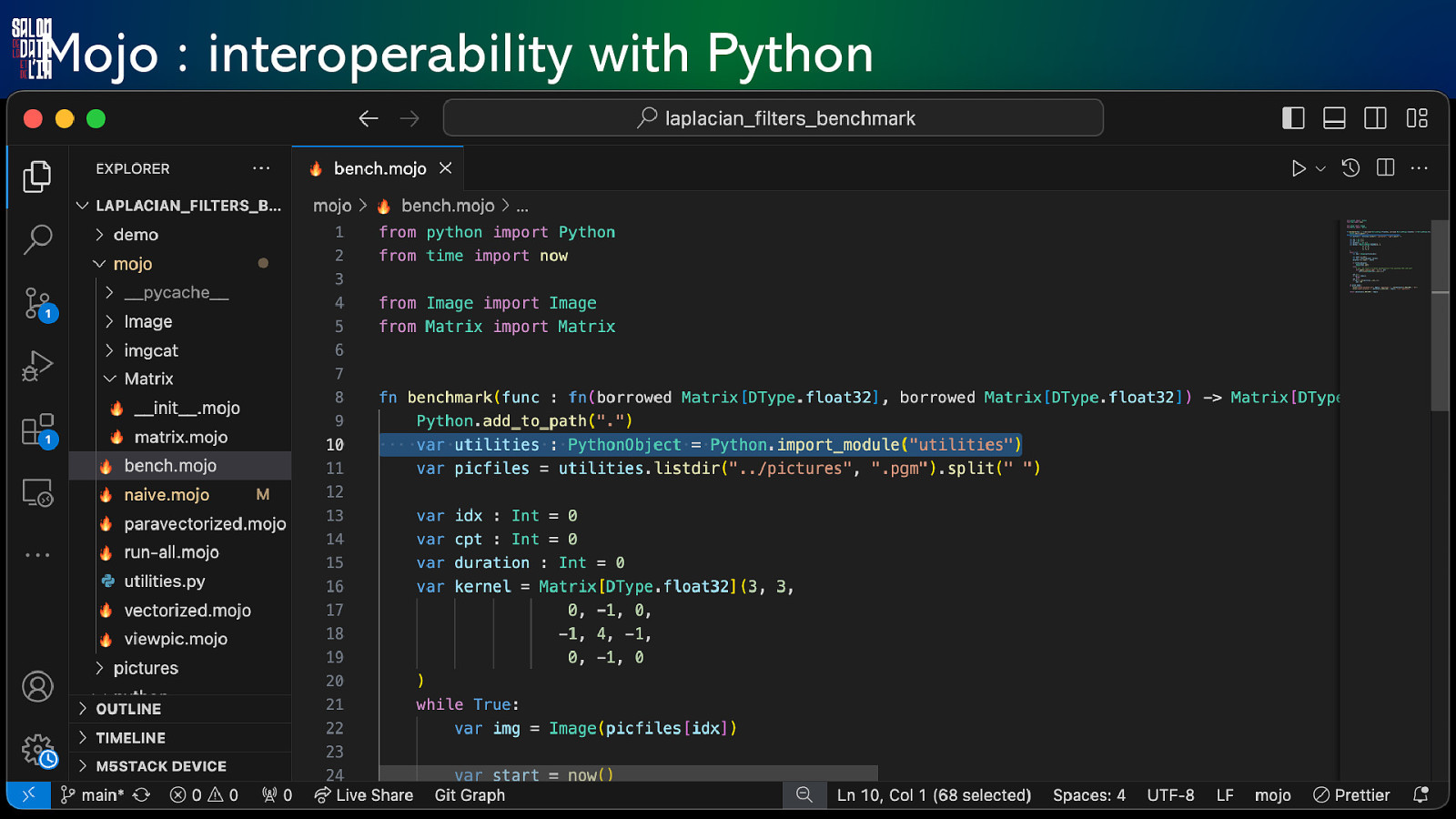
Mojo : interoperability with Python
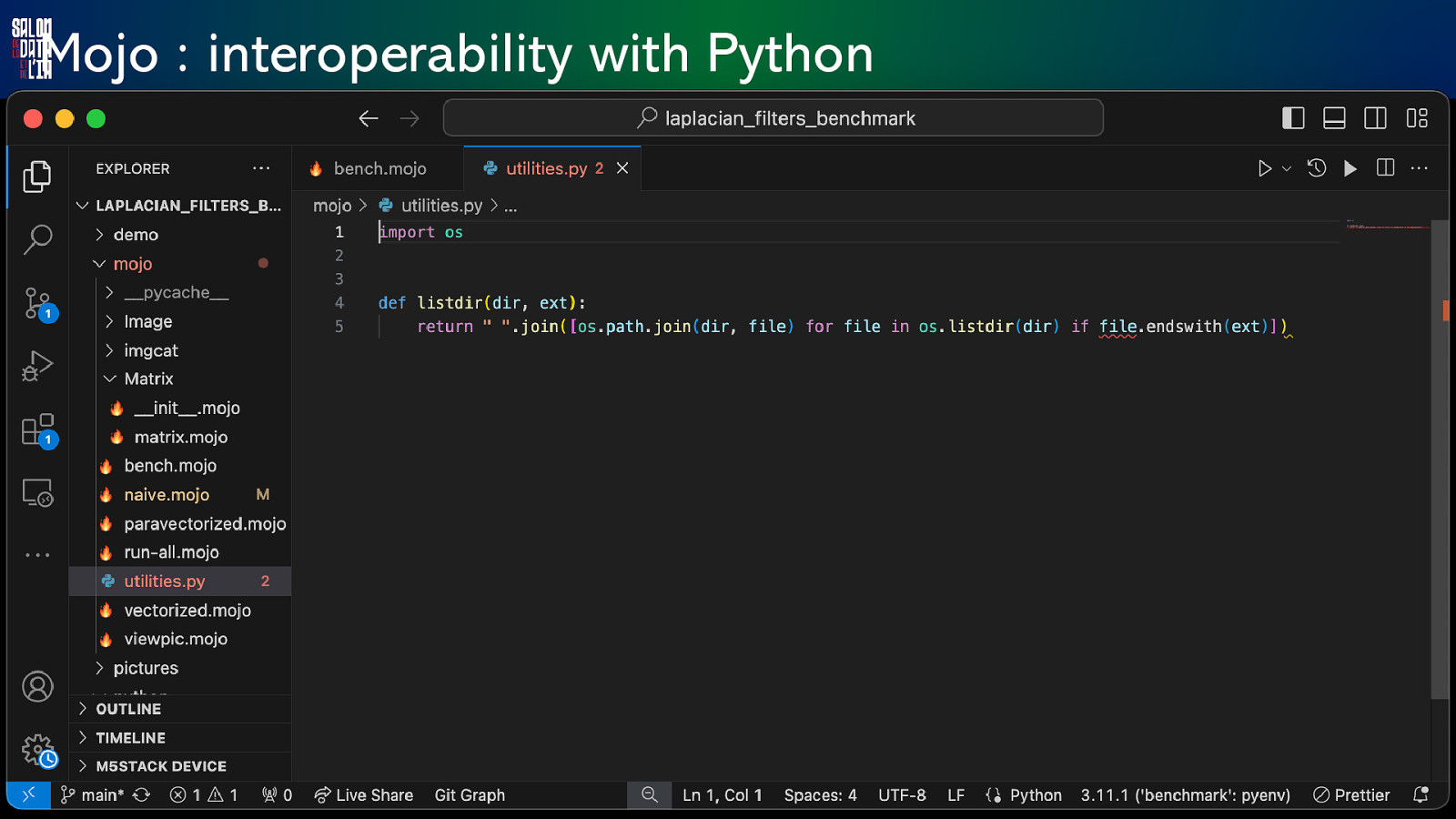
Mojo : interoperability with Python
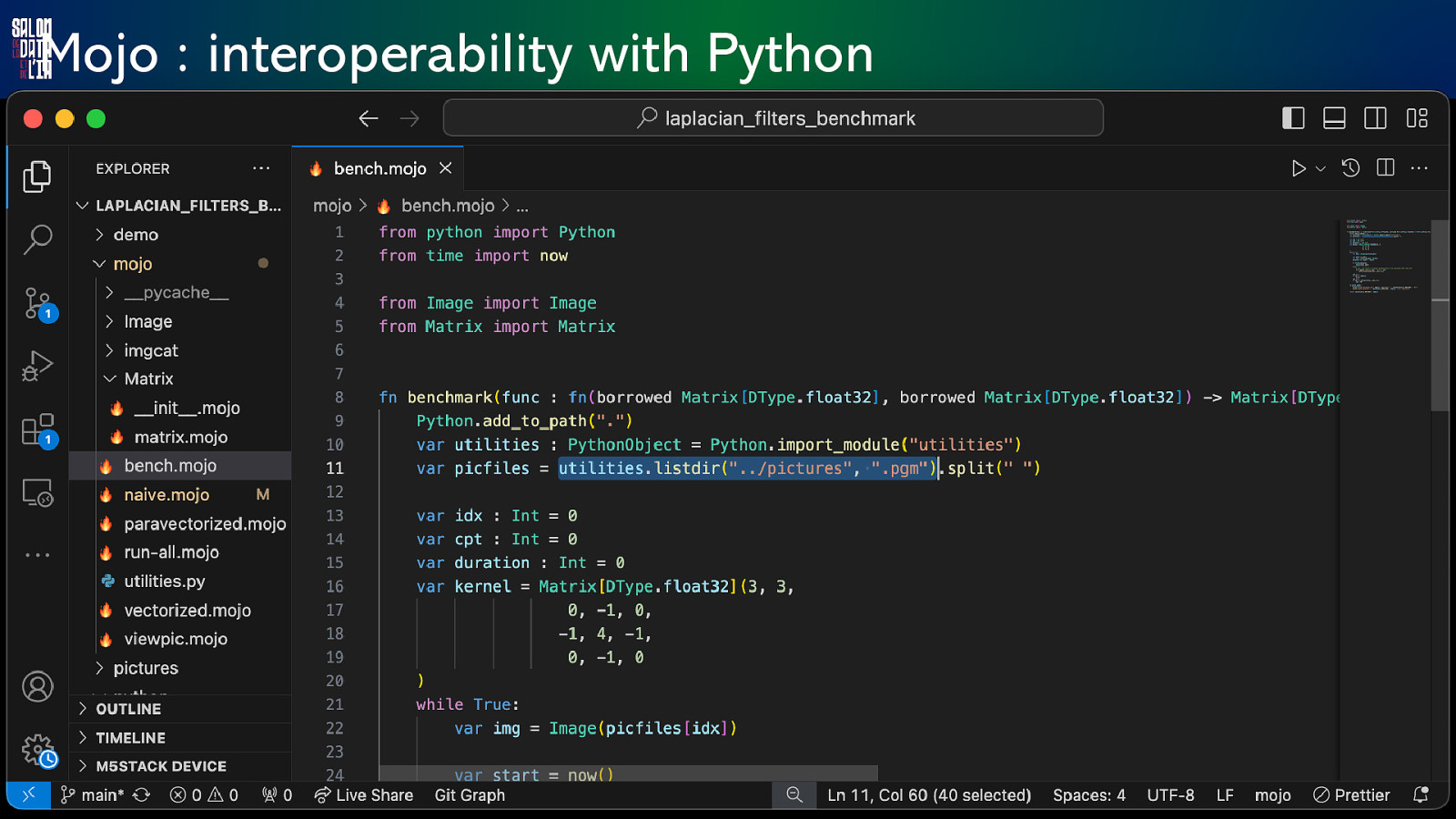
Mojo : interoperability with Python
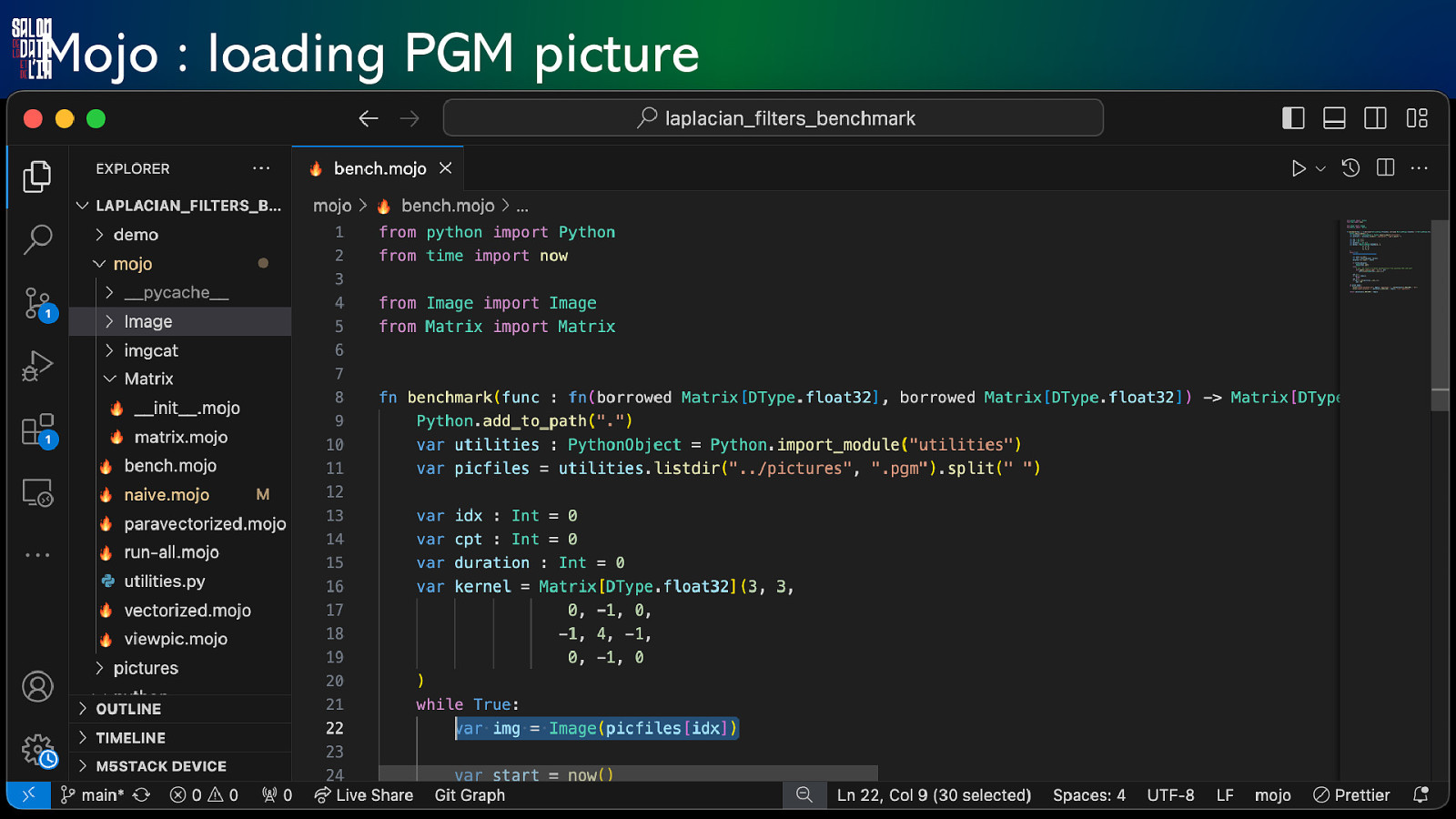
Mojo : loading PGM picture
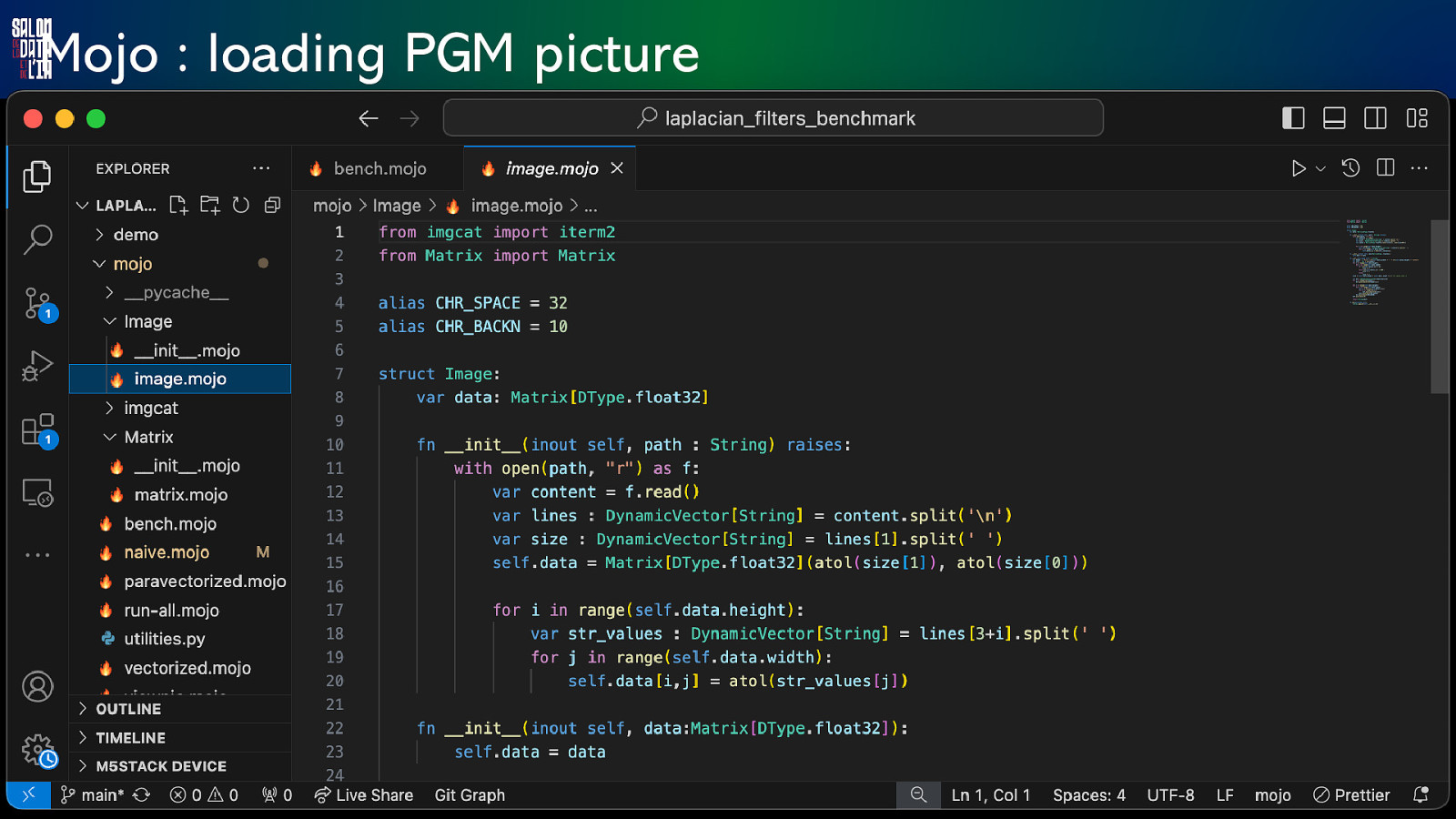
Mojo : loading PGM picture
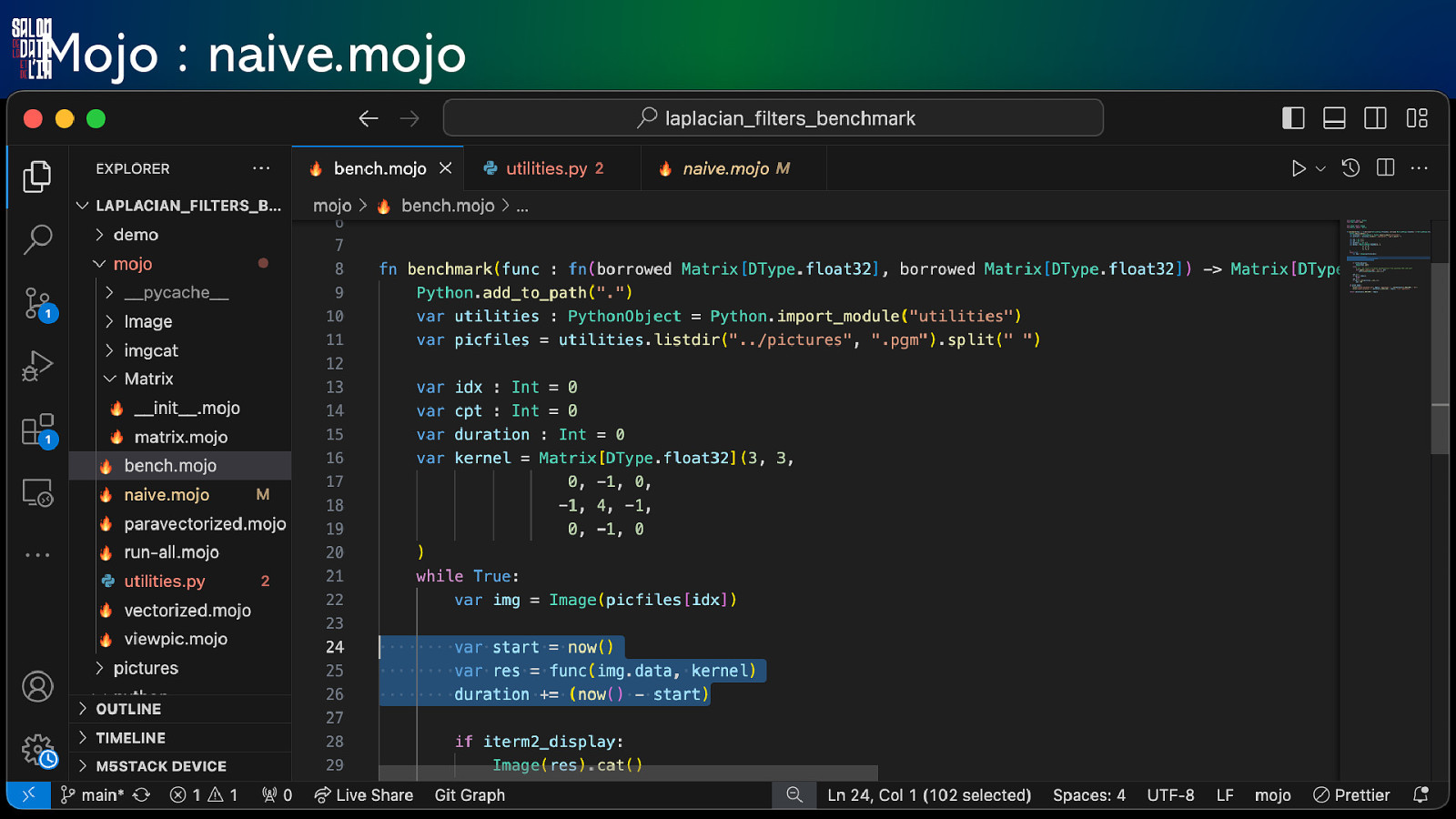
Mojo : naive.mojo
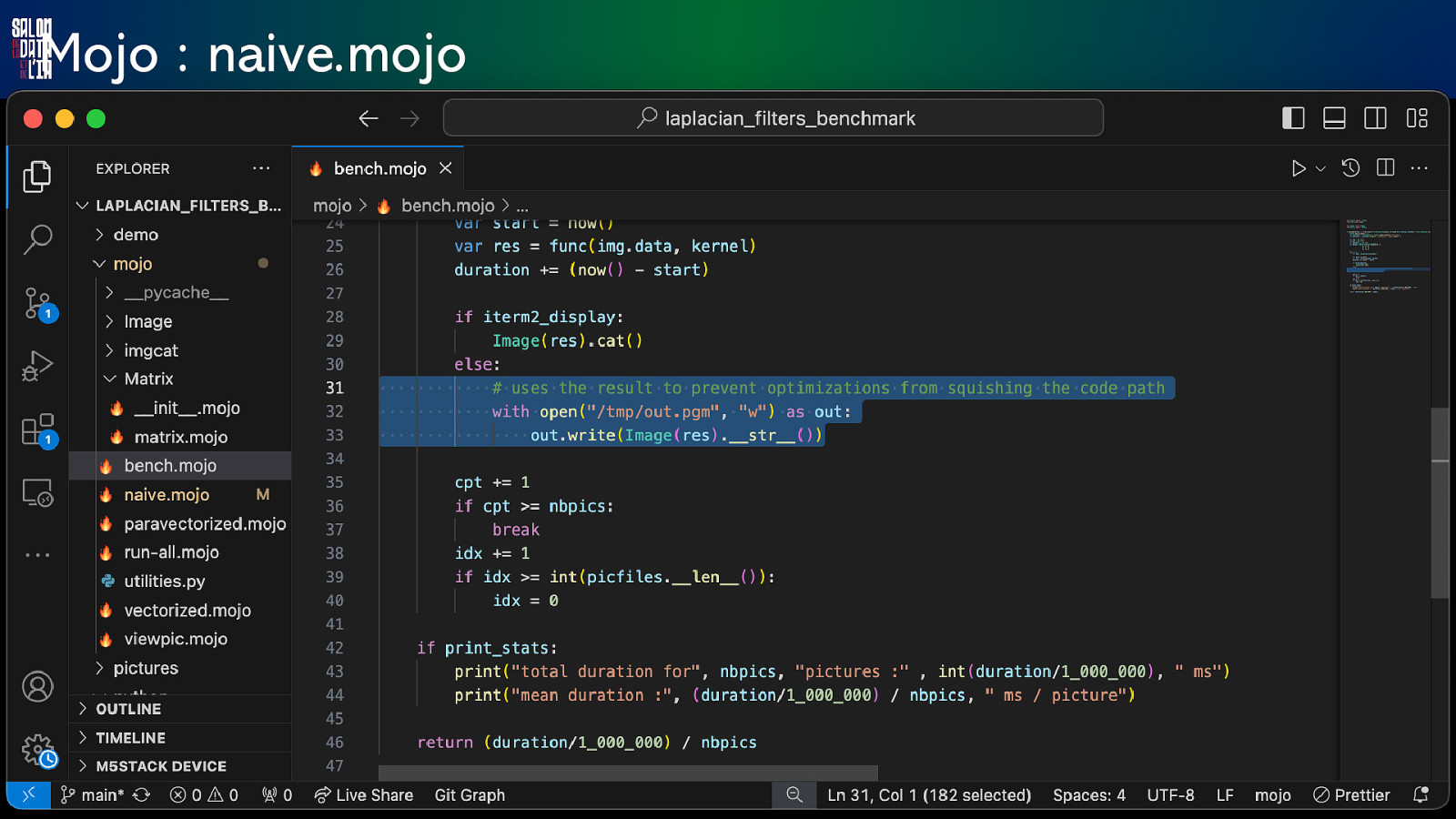
Mojo : naive.mojo

it’s demo time ! Let’s optimize !
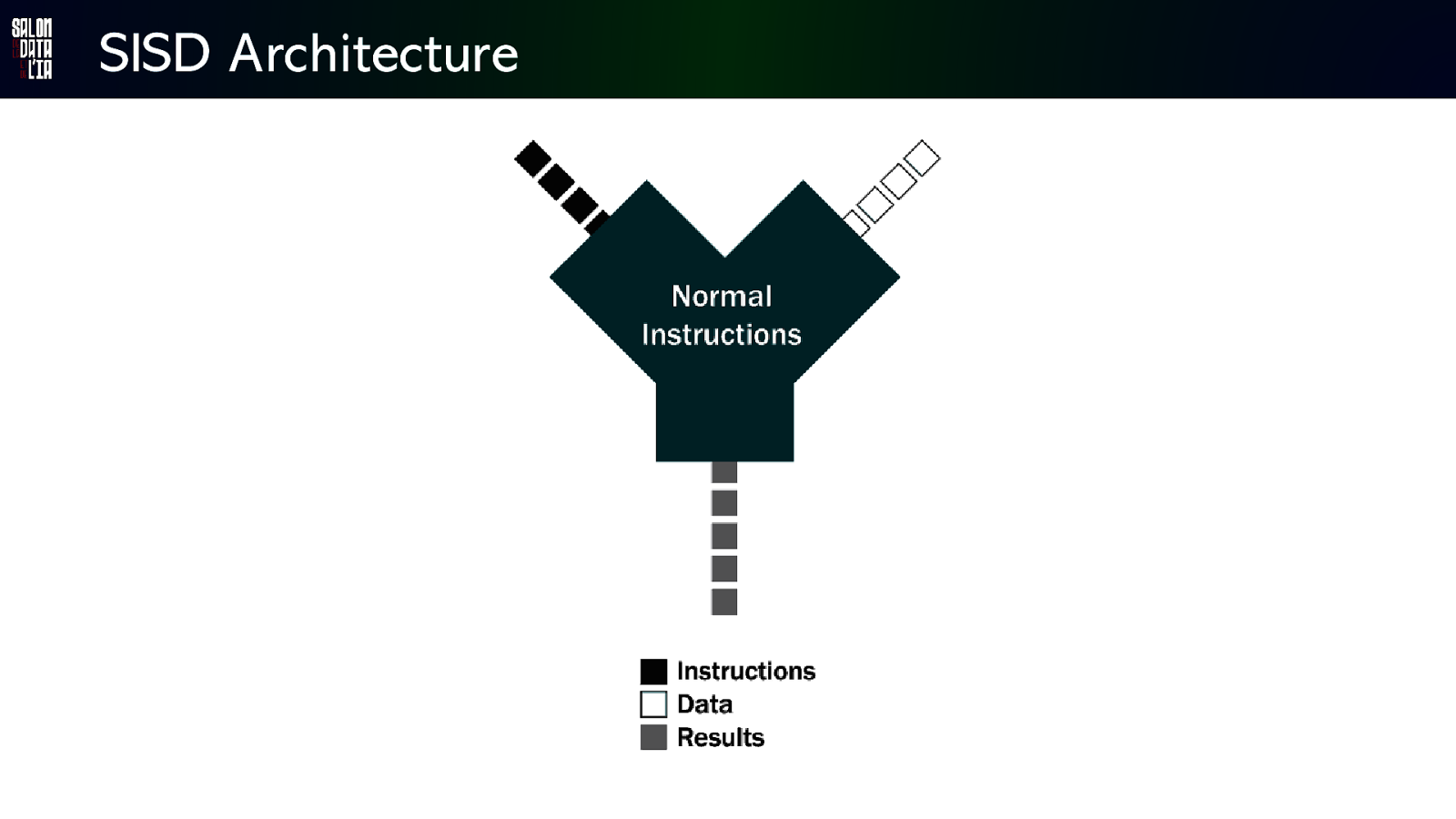
SISD Architecture
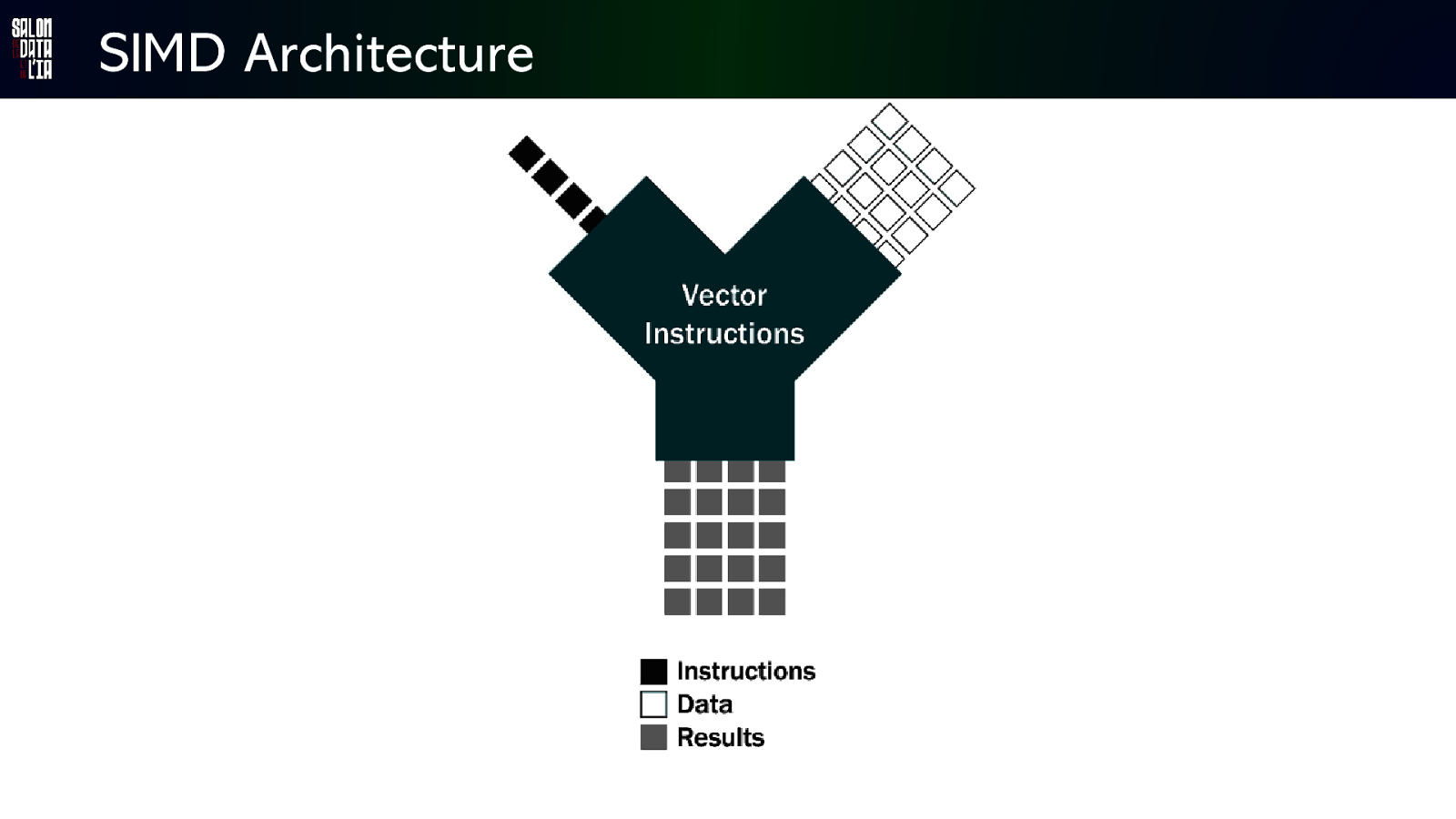
SIMD Architecture

Algorithm vectorization fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): for x in range(1, img.width-1): # For each pixel, compute the product elements wise var acc: Float32 = 0 for k in range(3) : for l in range(3): acc += img[y-1+k, x-1+l] * kernel[k, l] # Normalize the result result[y, x] = min(255, max(0, acc)) return result

Algorithm vectorization alias nelts = simdwidthofDType.float32 x fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): for x in range(1, img.width-1): # For each pixel, compute the product elements wise var acc: Float32 = 0 for k in range(3) : for l in range(3): acc += img[y-1+k, x-1+l] * kernel[k, l] # Normalize the result result[y, x] = min(255, max(0, acc)) return result
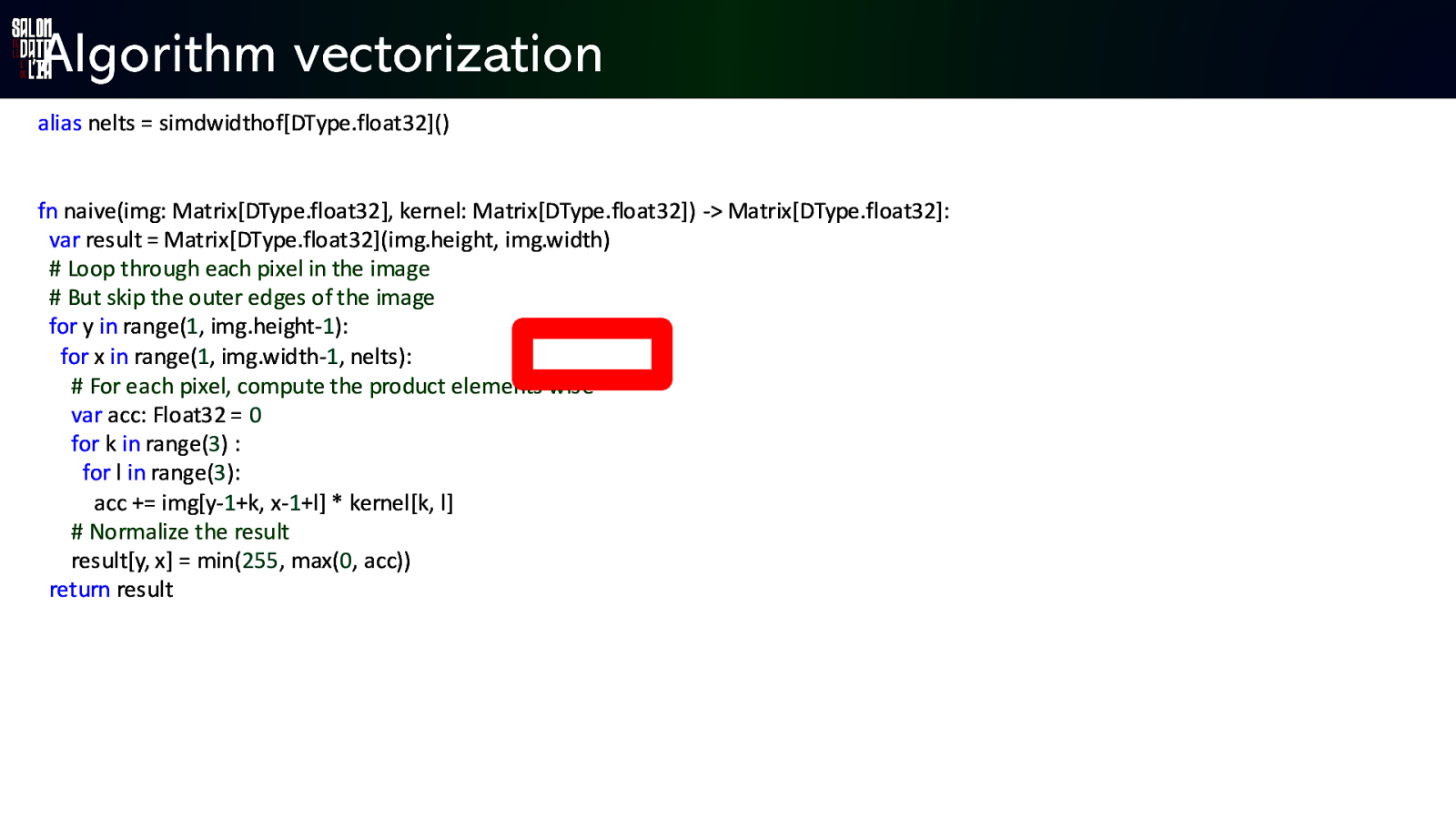
Algorithm vectorization alias nelts = simdwidthofDType.float32 fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): for x in range(1, img.width-1, nelts): # For each pixel, compute the product elements wise var acc: Float32 = 0 for k in range(3) : for l in range(3): acc += img[y-1+k, x-1+l] * kernel[k, l] # Normalize the result result[y, x] = min(255, max(0, acc)) return result
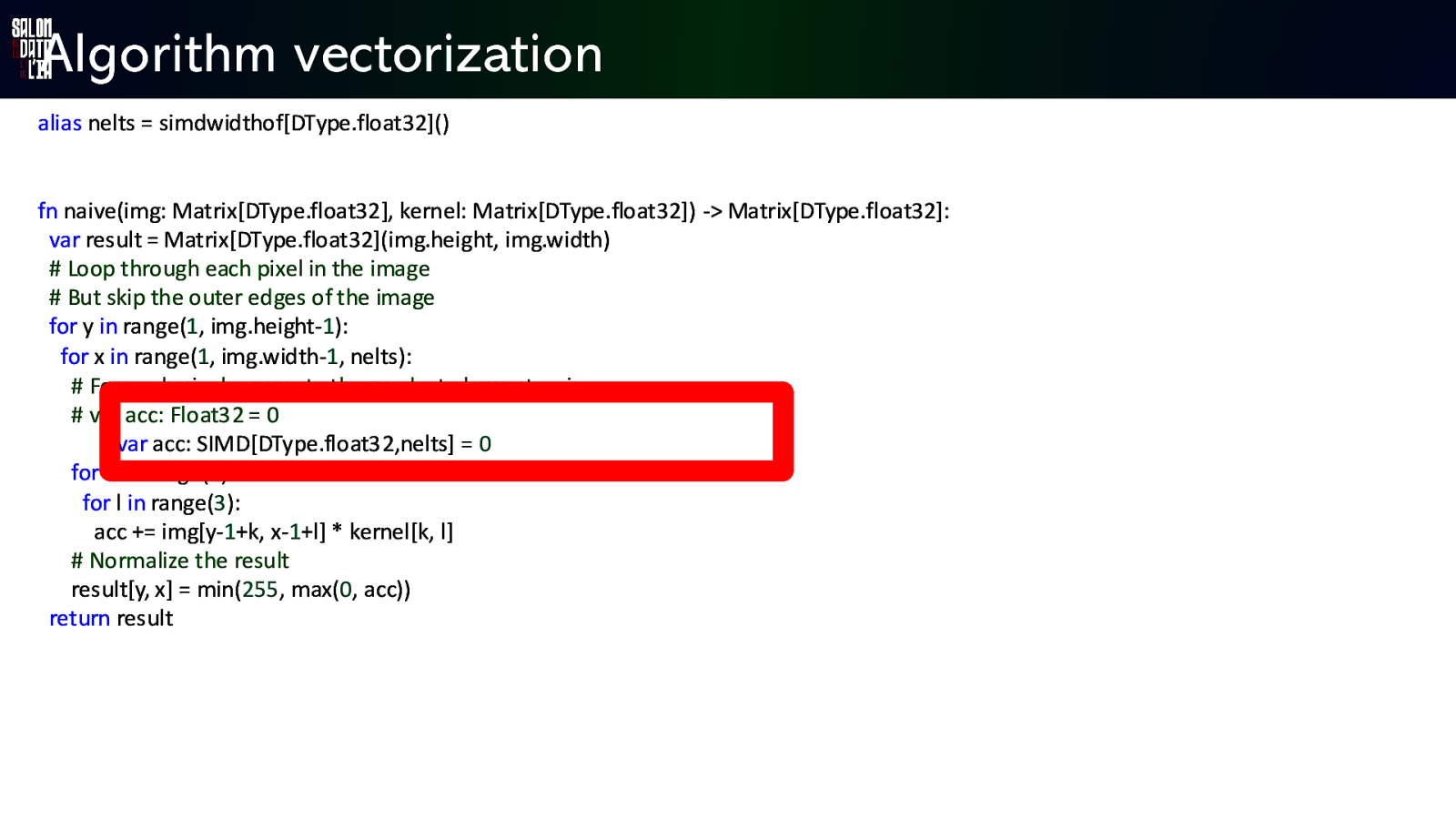
Algorithm vectorization alias nelts = simdwidthofDType.float32 fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): for x in range(1, img.width-1, nelts): # For each pixel, compute the product elements wise # var acc: Float32 = 0 var acc: SIMD[DType.float32,nelts] = 0 for k in range(3) : for l in range(3): acc += img[y-1+k, x-1+l] * kernel[k, l] # Normalize the result result[y, x] = min(255, max(0, acc)) return result

Algorithm vectorization fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): for x in range(1, img.width-1, nelts): # For each pixel, compute the product elements wise # var acc: Float32 = 0 var acc: SIMD[DType.float32,nelts] = 0 for k in range(3) : for l in range(3): # acc += img[y-1+k, x-1+l] * kernel[k, l] acc += img.simd_load[nelts](y-1+k, x-1+l) * kernel[k, l] # Normalize the result # result[y, x] = min(255, max(0, acc)) result.simd_store[nelts](y, x, min(255, max(0, acc))) return result

Algorithm vectorization fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): for x in range(1, img.width-1, nelts): # For each pixel, compute the product elements wise # var acc: Float32 = 0 var acc: SIMD[DType.float32,nelts] = 0 for k in range(3) : for l in range(3): # acc += img[y-1+k, x-1+l] * kernel[k, l] acc += img.simd_load[nelts](y-1+k, x-1+l) * kernel[k, l] # Normalize the result # result[y, x] = min(255, max(0, acc)) result.simd_store[nelts](y, x, min(255, max(0, acc))) # Handle remaining elements with scalars. for n in range(nelts * (img.width-1 // nelts), img.width-1) : var acc: Float32 = 0 for k in range(3) : for l in range(3): acc += img[y-1+k, n-1+l] * kernel[k, l] result[y, n] = min(255, max(0, acc)) return result

Algorithm vectorization alias nelts = simdwidthofDType.float32 fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): @parameter fn dot[nelts: Int](x: Int): # For each pixel, compute the product elements wise var acc: SIMD[DType.float32,nelts] = 0 for k in range(3) : for l in range(3): acc += img.simd_load[nelts](y-1+k, x-1+l) * kernel[k, l] # Normalize the result result.simd_store[nelts](y, x, min(255, max(0, acc))) vectorizedot, nelts return result

Algorithm vectorization alias nelts = simdwidthofDType.float32 fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): @parameter fn dot[nelts: Int](x: Int): # For each pixel, compute the product elements wise var acc: SIMD[DType.float32,nelts] = 0 for k in range(3) : for l in range(3): acc += img.simd_load[nelts](y-1+k, x-1+l) * kernel[k, l] # Normalize the result result.simd_store[nelts](y, x, min(255, max(0, acc))) vectorizedot, nelts return result

Algorithm vectorization alias nelts = simdwidthofDType.float32 fn naive(img: Matrix[DType.float32], kernel: Matrix[DType.float32]) -> Matrix[DType.float32]: var result = Matrix[DType.float32](img.height, img.width) # Loop through each pixel in the image # But skip the outer edges of the image for y in range(1, img.height-1): @parameter fn dot[nelts: Int](x: Int): # For each pixel, compute the product elements wise var acc: SIMD[DType.float32,nelts] = 0 for k in range(3) : for l in range(3): acc += img.simd_load[nelts](y-1+k, x+l) * kernel[k, l] # Normalize the result result.simd_store[nelts](y, x+1, min(255, max(0, acc))) vectorizedot, nelts return result

• Far from stable • Compilation AOT or JIT • Python friendly but not Python Recap • Dynamic Python vs Static Mojo • Python interoperability • Predictable behavior with semantic ownership • Low level optimization • Blazingly fast

Mojo The next AI language ?

Conclusion • Python is not yet dead ! But he moves slowly • This is a great team ! Will they be able to deploy their platform strategy ? • Will they be able to unite a community? To be open-source or not to be

Jean-Luc Tromparent Principal Engineer @ https://linkedin.com/in/jltromparent Merci ! https://github.com/jiel/laplacian_filters_benchmark https://noti.st/jlt/fBMjCq